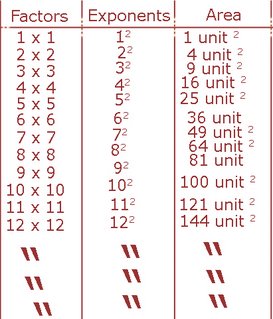
I will show you just how many countries are showing up,

Wow. This is why I would like to mention a few points. I love your enthusiasm. I want it to continue. Please for some of the comments you leave use the chat boxes provided to you. comments on peoples blogs must be polite and have no hidden meanings. You are excellent commenters on other peoples scribe posts. I think you do this better then any group I have ever worked with. Please do not stop commenting. Just think before you comment!
I encourage you to strive for excellence and have fun with your blog. It is a legacy that will remain here forever. Please use this tool wisely.
Now with that over I would like to say that the quality of the scribe lately has be beyond my expectations. You are to be congratulated on your terrific work and effort. Keep it going.
Please make note that your first Growing Posts will take place in December. I will keep you informed.
Once again. Remember you have an audience. This blog is an extension of the classroom. Stay in control.
Thank You
Mr. Harbeck